Introduction
Revised 5 March 2023
There is the well-known story of the farmer who noticed waterlilies on his pond which doubled in size every month. To start with, the waterlilies covered only a small area of the pond and the farmer said “to hell with it”. The farmer delayed taking care of the waterlilies and eventually the waterlilies covered the entire pond. How many months ago did the waterlilies cover 25% of the pond?
There is also the story of the peasant who, when asked by the Sultan what gift he desired in return for saving the life of his daughter, replied that all he desired was to be paid in grains of wheat, but with one condition. On the first day he should be paid one grain of wheat and for each day hence until all the squares on the Sultan's chess board had been marked off for each day, he should receive double the number of grains of the previous day. The puzzled Sultan agreed to these terms and complied with the condition of the gift. How soon afterwards did the Sultan request the peasant to choose an alternative gift?
In the 1970s, Professor Al Bartlett (2004) realised that many college and university students did not have an intuitive grasp of exponential growth and its implications for the future of humanity. Far too many students were unable to provide correct answers to similar questions as above. Al Bartlett subsequently devoted a great deal of time and energy over several decades educating students and the public as to the implications of exponential growth. This sub-section provides a non-mathematical summary of the essential properties of exponential growth.
First of all, a few definitions. If a quantity increases in size over time, it is said to be undergoing growth. If the quantity is decreasing in size over time, it is said to be undergoing decay.
If a quantity is always increasing (or decreasing), but the changes do not have the regularity of either linear or exponential change, the growth (or decay) is said to be monotonic or continuous.
Linear growth occurs when an entity increases by a fixed amount of the original quantity over each time interval. For example, an entity of 100 units increases by 10 units per year. At the end of 10 years, the entity has accumulated to 200 units - the original entity of 100 units plus 10 units each year for 10 years.
Take the previous example with an entity of 100 units and apply a growth rate where the entity has grown 10% larger by the end of each year. At the end of the first year the entity has grown to 110 units. At the end of the second year the entity has grown to 121 units (the extra 11 unit is 10% of 110 units). At the end of the third year the entity has grown to 132.1 units (the extra 12.1 units is 10% of 121 unit) and so on. By the end of the tenth year the entity has grown to 259.4 units. By the end of the seventh year the entity had grown to to almost 195 units.
Figure 1 shows an entity undergoing exponential growth versus linear growth. An entity undergoing a low rate of exponential growth will always grow larger and more rapidly over time than the same entity undergoing linear growth. The disruption is the difference in growth after exponential growth has surpassed linear growth.
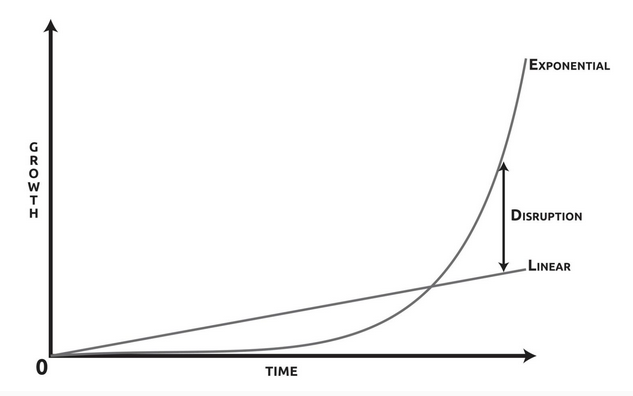
Figure 1: Exponential versus Linear Growth
The rate of exponential growth can vary, such as with population growth. If the rate of exponential growth fluctuates over time and the population is monotonically increasing, then the population is still said to be growing exponentially.
The doubling time of any entity which is growing is the time interval over which that entity doubles in size. Given a continuous rate of exponential growth, a rule of thumb to estimate how many years it takes for that entity to double in size is approximately given by 72 divided by the rate of exponential growth. For example, an economy growing at 3% per year takes 72/3 = 24 years to double in size.
Take any stock of resources from which one unit is extracted over the first time interval, two units are extracted over the second time interval, four units are extracted over the third time interval, and so on. That time interval is the doubling time of extraction.
The number of units that are extracted over each doubling time can be listed as follows:
1, 2, 4, 8, 16, 32, 64, 128, 245, 512, 1024, etc.
Take the number of units extracted over any doubling time. The sum of all the units that have been previously extracted is only slightly less than the number of units extracted over the doubling time. If a resource is found and extracted at a constant exponential rate of 3%, then it takes only 24 years to extract more or less the same amount as that extracted since the resource was first found.
Going back to the question about the waterlilies. When the waterlilies covered 25% of the pond, it took one month to double in size to cover 50% of the pond and one more month to double in size again to cover the entire pond. When the waterlilies covered 25% of the pond, the farmer had only two moinths to attend to the waterlilies. A second question. When should the farmer have prevented the waterlilies from choking up his pond? This would also depend on how long it took to clear the waterlilies. There is an analogy here. When should action be taken to transition from fossil fuels to renewable energy and infrastructure when there is a time lag in making the transition?
What more we can learn from the properties of exponential growth? Given steady exponential growth in the extraction of resources, the absolute size of the stock of any resource has very little effect on the time it takes to exhaust the resource. If the original resource were twice as large, it would take only one more doubling time to exhaust the resource.
Delays in action are critical when exponential growth is involved. This applies to both population, energy, and other resources, including ecosystems. William Ophuls warned us back in 1977 that the time for concern about the potential exhaustion of a resource comes when no more than about 10% of the total has been used up. So far, this warning has been ignored.